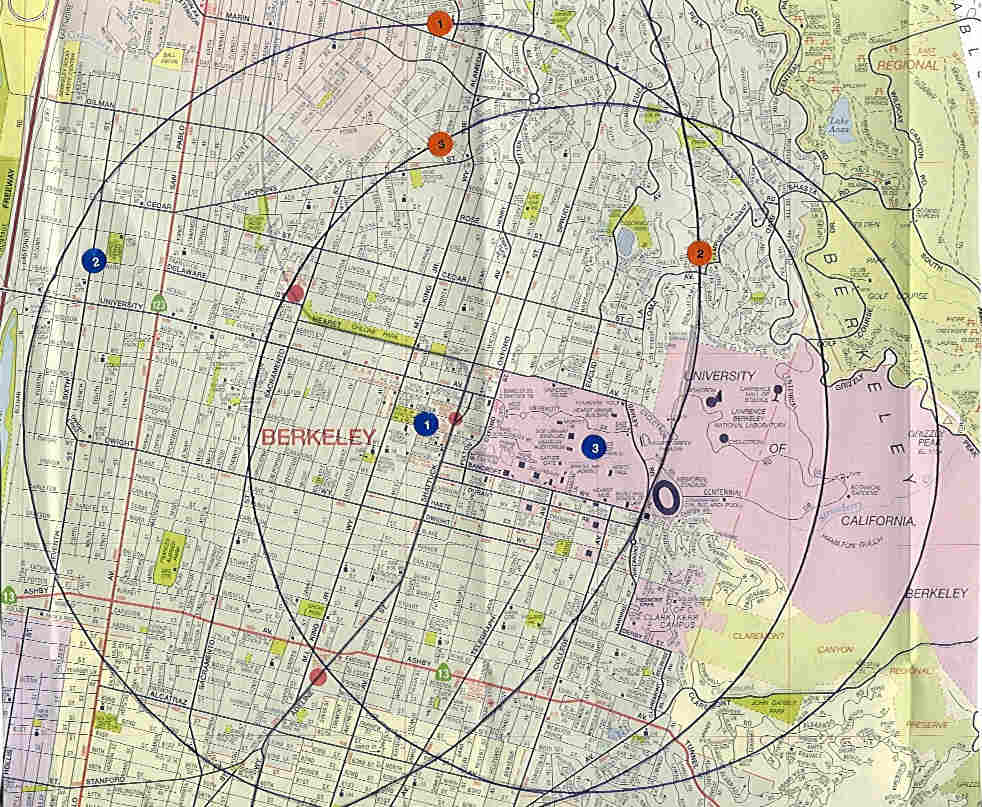
This is a simple triangulation problem in which you draw circles of the indicated radii from each of the three starting points. The point of intersection of the three circles is where you're supposed to go next. (I suppose they used three circles because with two, unless they're tangent to each other, you'd have two points of intersection and would be confused about which one to go to.)
1) The Christian Association is the YMCA at 2001 Allston Street (between Shattuck and Milvia) in Berkeley. 2974 somersaults, each advancing you 3 feet, takes you 8,922 feet, or 1.69 miles, from this location.
2) The first state to join the union was Delaware. Its nickname is "The First State" - there's a hint! So your starting point is 6th and Delaware Streets in Berkeley. Next you have to figure out how far 2.23333 nautical miles is.
Here's a definition to help you:
nautical
mile (nmi): A unit of distance used in navigation and based on
the
length of one minute of arc taken along
a great circle
Note 1: Because
the Earth is not a perfect sphere, various values have
been assigned to the nautical mile. The
value 1852 meters (6076.1 ft.)
has been adopted internationally.
Note 2: The
nautical mile is frequently confused with the geographical
mile, which is equal to 1 min of arc
on the Earth's equator (6087.15 ft).
So 2.2333 nautical miles equals 2.57 land miles.
{And for you land-lubbers, a "great circle" is defined as the points of intersection with the earth's surface of any plane passing through the exact center of the earth. There are 360 degrees in such a circle, and 60 minutes in each degree, so there are 21,600 nautical miles in a great circle. A nautical mile is approximately 15% longer than a statute (land) mile, so this works out to about 25,000 statute miles around the globe.}
3) The tallest structure on the UC Campus is the Campanile. The speed of light in a vacuum is 186,282 miles per second. A beam of light would therefore travel exactly 1.43 miles in 7.67653 x 10^-6 seconds.
(click on the map to see a larger version, then click "back" on your browser to return to this page)
We were amazed that the three circles actually do intersect at a precise point, which led us to:
THE NORTHWEST CORNER OF REMILLARD PARK, BERKELEY
In fact, to be very precise, the clue was at the top of a very tall rock formation in the park (people were doing technical climbing on it when we arrived). Our teammate Han bravely climbed to the top to retrieve the next clue.